Soru Sor
Sorunu sor hemen cevaplansın.
 ile gösterilir.
ile gösterilir.
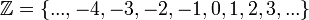
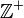 ile gösterilir ve aşağıdaki gibi tanımlıdır:
ile gösterilir ve aşağıdaki gibi tanımlıdır:
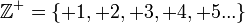
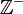 ile gösterilir. Cebirde çıkarma işlemi bu sayıların diğer tam sayılarla toplanması olarak ifade edilir.
ile gösterilir. Cebirde çıkarma işlemi bu sayıların diğer tam sayılarla toplanması olarak ifade edilir.
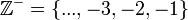
Tarih: 2014-03-26 22:00:00 Kategori: Matematik
Soru Tarat
Kitaptan sorunu tarat hemen cevaplansın.
Sorunu sor hemen cevaplansın.
Tam Sayı Nedir
Tam Sayılar
Tam sayılar eksi sonsuzdan artı sonsuza kadar giderler. Yani "0"ın iki yanından sonsuza kadar uzanırlar. Tam sayılar kümesi ile gösterilir.
ile gösterilir.
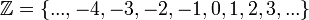
Pozitif Tam Sayılar
Başında "+" işareti bulunan veya bir şey bulunmayan tam sayılar pozitif tam sayılar adını alırlar. Sayı ekseninde (sayı doğrusunda) 0'ın sağ yanında yer alırlar. Tüm sayma sayıları pozitif tam sayılardır. Pozitif tam sayılar kümesi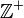 ile gösterilir ve aşağıdaki gibi tanımlıdır:
ile gösterilir ve aşağıdaki gibi tanımlıdır:
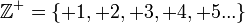
Negatif Tam Sayılar
Başında "-" işareti olan tam sayılar negatif tam sayılar adını alırlar. Sayı ekseninde 0'ın sol yanında yer alırlar. Negatif tam sayılar kümesi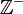 ile gösterilir. Cebirde çıkarma işlemi bu sayıların diğer tam sayılarla toplanması olarak ifade edilir.
ile gösterilir. Cebirde çıkarma işlemi bu sayıların diğer tam sayılarla toplanması olarak ifade edilir.
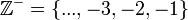
Tarih: 2014-03-26 22:00:00 Kategori: Matematik
Kitaptan sorunu tarat hemen cevaplansın.
Yorum Yapx
Tam Sayı Resimleri
-

4  5 yıl önce
Tam Sayı Nedir
5 yıl önce
Tam Sayı Nedir
0  5 yıl önce
Tam Sayılarda Toplama
5 yıl önce
Tam Sayılarda Toplama
0 Tam Sayı Sunumları
-

2 Dosyayı Göster5 yıl önceTam Sayılar Ödevi Slayt Sunum PPTXİndir : 52_tam-sayilar.pptx(Göster / Gizle) Sunum İçeriği: Düz metin (text) olarak..
1. Sayfa
DOĞAL SAYILAR TAM SAYILARÖğr. Gör. Mehmet Ali ZENGİN
2. Sayfa
KONU BAŞLIKLARI1. TEMEL KAVRAMLAR 2. SAYILARIN SINIFLANDIRILMASI 2.1. Doğal Sayılar 2.2. Tam Sayılar 2.2.1. Çift ve Tek Sayılar 2.2.2. Pozitif ve Negatif Sayılar 2.2.3. Ardışık Sayılar3. FAKTÖRİYEL KAVRAMI
3. Sayfa
1. Temel KavramlarRakam1 ve 8 hem birer rakam hem de birer sayıdır. Buna sayıları ifade etmek için kullanılan sembollere rakam denir.{0, 1,2, 3, 4, 5, 6, 7, 8, 9} kümesinin elemanları onluk sayma sisteminde kullanılan rakamlardır.SayıRakamların bir çokluk belirtecek şekilde bir araya getirilmesiyle oluşturulan ifadelere sayı denir.Uyarı: Tüm rakamlar birer sayıdır. Fakat her sayı bir rakam değildir!!!1 ve 8 hem birer rakam hem de birer sayıdır. Buna karşılık 18 bir sayıdır, fakat rakam değildir.
4. Sayfa
2. Sayıların Sınıflandırılması2.1. Doğal SayılarDoğal sayılar kümesi N harfi ile gösterilir.N = {0, 1,2, 3, ...} kümesinin elemanlarının her biri birer doğal sayıdır. Sıfır haricindeki doğal sayılara pozitif doğal sayılar ya da sayma sayıları denir. N+ sembolü ile gösterilir.N+ = {1,2, 3, ...} kümesinin elemanlarının her biri birer sayma sayısıdır.Örnek Soru 1: a ve b birer rakam olmak üzere,𝑎+10𝑏=12olduğuna gore, a nın alabileceği değerlerin toplamı kaçtır? A) 7 B) 9 C) 13 D) 19 E) 30
5. Sayfa
2. Sayıların Sınıflandırılması2.1. Doğal SayılarÖrnek Soru Çözümü : Bu eşitlikte a bir rakam olduğundan 𝟏𝟎 𝐛 bir doğal sayı olmalıdır. Bunun için, b rakamı 1,2, 5 olabilir.b = 1 için 𝑎+101=12 a = 2 b = 2 için 𝑎+102=12 a = 7b = 5 için 𝑎+105=12 a = 10 olduğundan a bir rakam değildir. Buna gore, a nın alabileceği değerlerin toplamı 2 + 7 = 9 bulunur.
6. Sayfa
2. Sayıların Sınıflandırılması2.1. Doğal SayılarÖrnek Soru 2: a ile b sayma sayısı olmak üzere,a + b = 13olduğuna göre, a.b çarpımının en büyük ve en küçük değerlerinin toplamı kaçtır?A) 42 B) 45 C) 51 D) 54 E) 56
7. Sayfa
2. Sayıların Sınıflandırılması2.1. Doğal SayılarÖrnek Soru 2 Çözüm: a + b = 13 eşitliğinde a ile b birbirine yaklaştıkça çarpımları büyür ve birbirinden uzaklaştıkça çarpımları küçülür. 7 + 6 = 13 için a.b = 7.6 = 42 12 + 1 = 13 için a.b = 12.1 = 12 olur.Buna göre, a.b çarpımının en büyük değeri 42 ve en küçük değeri 12 olduğundan, bu değerlerin toplamı 42 + 12 = 54 bulunur.
8. Sayfa
2. Sayıların Sınıflandırılması2.1. Doğal SayılarÖrnek Soru 3:a ile b doğal sayı olmak üzere, 4a + 5b = 50olduğuna göre, a sayısı kaç farklı değer alabilir?A) 2 B) 3 C) 4 D) 5 E) 6
9. Sayfa
2. Sayıların Sınıflandırılması2.1. Doğal SayılarÖrnek Soru 3 Çözüm: Önce a = 0 için b = 10 bulunur. Daha sonra a nın değerleri b nin katsayısı kadar artırılırsa b nin değerleri de a nın katsayıları kadarazalır.4a + 5b = 50 ↓ ↓ 0 10 5 6 10 2 15 –2 ∉ Nolduğundan a sayısı 3 farklı değer alır.
10. Sayfa
2. Sayıların Sınıflandırılması2.2. Tam SayılarTam sayılar kümesi Z harfi ile gösterilir. Z = {…, –3, –2, –1, 0, 1, 2, 3, …}kümesinin elemanlarının her biri birer tam sayıdır.Tam sayılar kümesi; negatif tam sayılar, pozitif tam sayılar ve sıfırın birleşim kümesine eşittir.Negatif tam sayılar: 𝑍− = {…, –2, –1}Pozitif tam sayılar: 𝑍+ = {1, 2, …}Buna gore, Z = 𝒁− ∪ 𝒁+ ∪ {0} dır. Uyarı : Sıfır bir tam sayıdır, ancak pozitif veya negatif değildir.
11. Sayfa
2. Sayıların Sınıflandırılması2.2. Tam SayılarÖrnek Soru 1: a ile b tam sayı olmak üzere;b ∈ 𝒁+ ve 𝐛=𝟐𝐚−𝟓𝐚 olduğuna göre, kaç farklı a sayısı vardır?A) 1 B) 2 C) 3 D) 4 E) 5
12. Sayfa
2. Sayıların Sınıflandırılması2.2. Tam SayılarÖrnek Soru 1 Çözüm: 𝐛=2𝑎−5𝑎=2𝑎𝑎−5𝑎=2−5𝑎a=1 için b = 2−51 = 2-5=-3 ∉ 𝒁+ a=5 için b = 2−55 = 2-1=1 ∈ 𝒁+ a=-1 için b = 2−5−1 = 2+5=7 ∈ 𝒁+ a=-5 için b = 2−5−5 = 2+1=3 ∈ 𝒁+ olduğundan 3 farklı a sayısı vardır.
13. Sayfa
2. Sayıların Sınıflandırılması2.2. Tam SayılarÖrnek Soru 2: Rakamları farklı üç basamaklı en büyük negatif tam sayı ile iki basamaklı rakamları farklı en küçük tam sayının toplamı kaçtır? A) –200 B) –201 C) –202 D) –203 E) –204Çözüm: (–102) + (–98) = –200 olur.style.visibilityppt_xppt_y
14. Sayfa
2. Sayıların Sınıflandırılması2.2. Tam SayılarÖrnek Soru 3: a, b ve c negatif tam sayı olmak üzere, 2a = 3b ve 4b = 5colduğuna göre, a + b + c toplamının en büyük değeri kaçtır?A) –20 B) –23 C) –27 D) –33 E) –42
15. Sayfa
2. Sayıların Sınıflandırılması2.2. Tam SayılarÖrnek Soru 3 Çözüm: 2a = 3b ve 4b = 5c olduğundan, 8a = 12b = 15c olur.Burada a = –15, b = –10 ve c = –8 değerini aldığında a + b + c toplamı en çok: (–15) + (–10) + (–8) = –33 bulunur.
16. Sayfa
2.2 Tam Sayı Çeşitleri2.2.1. Çift ve Tek SayılarBirler basamağı {0, 2, 4, 6, 8} rakamlarından biri olan tam sayılara çift sayı, {1, 3, 5, 7, 9} rakamlarından biri olan sayılara tek sayı denir.Ç çift bir sayıyı, T tek bir sayıyı göstermek üzere;Ç ± Ç = Ç Ç.Ç = Ç Ç𝑛 = Ç (n ∈ N+)T ± T = Ç T.T = T 𝑇𝑛 = T (n ∈ N+)Ç ± T = T Ç.T = ÇÖrnek Soru 1 : Aşağıdaki sayıların hangisi bir tek sayıdır?A) 20094 – 1979 B) 923 + 139 C) 7. 43 D) 28 + 39 + 510 E) 5(45 – 54)
17. Sayfa
2.2 Tam Sayı Çeşitleri2.2.1. Çift ve Tek SayılarÖrnek Soru Çözüm 1 : A) 20094 → T ve 1979 → T ⇒ T – T = ÇB) 923 → T ve 139→ T ⇒ T + T = ÇC) 7 → T ve 43 → Ç ⇒ T.Ç= ÇD) 28 → Ç, 39 → T ve 510 → T ⇒ Ç+ T + T = ÇE) 5 → T, 45 → Ç, 54 → T ⇒ T(Ç – T)⇒ T.T = T olur.
18. Sayfa
2.2 Tam Sayı Çeşitleri2.2.1. Çift ve Tek SayılarÖrnek Soru 2 : a, b ve c birer tam sayı olmak üzere, 3(a.b) + 5a = 4c + 1olduğuna göre, aşağıdakilerden hangisi doğrudur?A) a çift, b tek sayıdır. B) a ve b tek sayıdır.C) a ve b çift sayıdır. D) a tek, b çift sayıdır. E) a + b çift sayıdır.
19. Sayfa
2.2 Tam Sayı Çeşitleri2.2.1. Çift ve Tek SayılarÖrnek Soru Çözüm 2 : 3.a.b + 5a = 4c + 1 ⇒ a(3b + 5) = 4c + 1 olur.4c + 1 daima tek sayı olduğundan, a ve (3b + 5) sayılarının her ikisinin de tek olması gerekir.3b + 5 tek sayı ise b cift sayıdır.Buna gore, a tek, b çift sayı olmalıdır.
20. Sayfa
2.2 Tam Sayı Çeşitleri2.2.2. Pozitif ve Negatif SayılarSayı doğrusu üzerinde sıfırın sağında kalan sayılara pozitif sayılar, solunda kalan sayılara negatif sayılar denir.(+) pozitif bir sayıyı, (–) negatif bir sayıyı ve n bir tam sayıyı göstermek üzere,(+) . (+) = (+)(–) . (–) = (+)(–) . (+) = (–)(+) . (–) = (–) olur.(+)(+)=+, (−)(−)=(+), (+)(−)=(−), (−)(+)=(−)(+)n=(+), (−)2n=(+), (−)2n−1=(-)
21. Sayfa
2.2 Tam Sayı Çeşitleri2.2.2. Pozitif ve Negatif Sayılarİşlem önceliği ;Üslü NiceliklerParantez İçiÇarpma ve BölmeToplama ve ÇıkarmaNot : Aynı öncelikli işlemler varsa soldan sağa doğru işlem yapılır.
22. Sayfa
2.2 Tam Sayı Çeşitleri2.2.2. Pozitif ve Negatif SayılarÖrnek Soru 1 : 9 + 6 : (–3) – [–7 – (–2 + 1)]işleminin sonucu kaçtır?A) –6 B) –3 C) 0 D) 6 E) 13
23. Sayfa
2.2 Tam Sayı Çeşitleri2.2.2. Pozitif ve Negatif SayılarÖrnek Soru Çözüm 1 : 9 + 6 : (–3) – [–7 – (–2 + 1)]= 9 + 6 : (–3) – (–7 + 1)= 9 + 6 : (–3) + 6= 9 -2+6=7+6=13
24. Sayfa
2.2 Tam Sayı Çeşitleri2.2.2. Pozitif ve Negatif SayılarÖrnek Soru 2 : –2 – 24 : [6 + 3.1 – 3:1] – 5işleminin sonucu kaçtır?A) –11 B) –9 C) –7 D) –5 E) –4
25. Sayfa
2.2 Tam Sayı Çeşitleri2.2.2. Pozitif ve Negatif SayılarÖrnek Soru Çözüm 2 : –2 – 24 : [6 + 3.1 – 3:1] – 5= –2 – 24 : (6 + 3 – 3) – 5= –2 – 24 : 6 – 5= –2 – 4 – 5 = – 6 – 5= –11
26. Sayfa
2.2 Tam Sayı Çeşitleri2.2.2. Pozitif ve Negatif SayılarÖrnek Soru 3 : 18 – [8 + (–19 : (–1))] : (–9)işleminin sonucu kaçtır?A) 15 B) 18 C) 21 D) 24 E) 27
27. Sayfa
2.2 Tam Sayı Çeşitleri2.2.2. Pozitif ve Negatif SayılarÖrnek Soru Çözüm 3 : 18 – [8 + (–19 : (–1))] : (–9)= 18 - [8 + 19] : (-9)= 18 – 27 : (-9)= 18 + 3= 21
28. Sayfa
2.2 Tam Sayı Çeşitleri2.2.3. Ardışık SayılarBelli bir kurala göre aynı miktarda artan veya azalan sayı dizilerine ardışık sayılar denir.n bir tam sayı olmak üzere;Ardışık tam sayılar n, n + 1, n + 2, …Ardışık çift sayılar 2n, 2n + 2, 2n + 4, …Ardışık tek sayılar 2n – 1, 2n + 1, 2n + 3, …5 in katı olan a rdışık sayılar 5n, 5n + 5, 5n + 10, … şeklinde gösterilebilir.
29. Sayfa
2.2 Tam Sayı Çeşitleri2.2.3. Ardışık SayılarArdışık sayılar dizisinin terim sayısı, 𝑆𝑜𝑛 𝑇𝑒𝑟𝑖𝑚−İ𝑙𝑘 𝑇𝑒𝑟𝑖𝑚𝐴𝑟𝑡𝚤ş 𝑀𝑖𝑘𝑡𝑎𝑟𝚤 + 1Örnek Soru : 33, 37, 41, … , 97 dizisinin kac terimi vardır?15 B) 16 C) 17 D) 18 E) 19 𝑆𝑜𝑛 𝑇𝑒𝑟𝑖𝑚−İ𝑙𝑘 𝑇𝑒𝑟𝑖𝑚𝐴𝑟𝑡𝚤ş 𝑀𝑖𝑘𝑡𝑎𝑟𝚤 + 1 97−334 + 1 = 17 style.visibilityppt_xppt_y
30. Sayfa
2.2 Tam Sayı Çeşitleri2.2.3. Ardışık SayılarSonlu ardışık pozitif tam sayıların toplamı T olsun.T = (Terim Sayısı). (𝑆𝑜𝑛 𝑡𝑒𝑟𝑖𝑚+İ𝑙𝑘 𝑡𝑒𝑟𝑖𝑚2) Örnek Soru : 4 + 7 + 10 + … + 28 toplamının sonucu kaçtır?124 B) 130 C) 134 D) 140 E) 144 T= (𝑆𝑜𝑛 𝑇𝑒𝑟𝑖𝑚−İ𝑙𝑘 𝑇𝑒𝑟𝑖𝑚𝐴𝑟𝑡𝚤ş 𝑀𝑖𝑘𝑡𝑎𝑟𝚤 + 1 ) . (𝑆𝑜𝑛 𝑡𝑒𝑟𝑖𝑚+İ𝑙𝑘 𝑡𝑒𝑟𝑖𝑚2) = (28−43 + 1 ) . (28+42) = 9.16 = 144 style.visibilityppt_xppt_y
31. Sayfa
2.2 Tam Sayı Çeşitleri2.2.3. Ardışık SayılarÖrnek Soru 1 : Ardışık üç pozitif çift sayının toplamı 54 tür.Bu sayıların en büyüğü kaçtır?A) 16 B) 18 C) 20 D) 22 E) 24
32. Sayfa
2.2 Tam Sayı Çeşitleri2.2.3. Ardışık SayılarÖrnek Soru Çözüm 1 : En küçük sayı 2n olsun.2n + (2n + 2) + (2n + 4) = 546n + 6 = 546n = 48 ⇒ n = 8olduğundan en büyük, 2n+4 = 16 + 4 = 20 bulunur.
33. Sayfa
2.2 Tam Sayı Çeşitleri2.2.3. Ardışık SayılarÖrnek Soru 2 : (a + 5) ve (2a – 3) ardışık iki tek sayı olduğuna göre,a nın alabileceği değerlerin toplamı kactır?A) 15 B) 16 C) 17 D) 18 E) 19
34. Sayfa
2.2 Tam Sayı Çeşitleri2.2.3. Ardışık SayılarÖrnek Soru Çözüm 2 : Ardışık iki tek sayı arasındaki fark 2 olduğundan;(a + 5) – (2a – 3) = 2 veya (2a – 3) – (a + 5) = 2 olmalıdır.(a + 5) – (2a – 3) = 2 ⇒ a + 5 – 2a + 3 = 2 ⇒ a = 6(2a – 3) – (a + 5) = 2 ⇒ 2a – 3 – a – 5 = 2 ⇒ a = 10olduğundan, a nın alabileceği değerlerin toplamı: 6 + 10 = 16 bulunur.
35. Sayfa
3. Faktöriyel Kavramı1 den n ye kadar olan doğal sayıların çarpımına n faktöriyel denir ve n! şeklinde gösterilir.n! = n.(n – 1).(n – 2). ……0! = 1 olarak tanımlanır.1! = 12! = 2.1 = 23! = 3.2.1 = 64! = 4.3.2.1 = 24 n! = n(n – 1)!6! = 6.5.4.3.2.1 olarak yazılabildiği gibi6! = 6.5! veya 6! = 6.5.4! olarak da yazılabilir.
36. Sayfa
3. Faktöriyel KavramıÖrnek Soru 1 : 14!−13!12!+11!işleminin sonucu kaçtır?A) 126 B) 132 C) 144 D) 152 E) 156
37. Sayfa
3. Faktöriyel KavramıÖrnek Soru Çözüm 1 : 14!−13!12!+11! = 14.13!−13!12.11!+11! = 13!(14−1)11!(12+1) = 13!.1311!.13 = 13!11! =13.12.11!11! = 13.12 = 156
38. Sayfa
3. Faktöriyel KavramıÖrnek Soru 2 : 0! + 1! + 2! + 3! + … + 28!toplamının birler basamağındaki rakam kaçtır?A) 1 B) 2 C) 3 D) 4 E) 5
39. Sayfa
3. Faktöriyel KavramıÖrnek Soru Çözüm 1 : Toplamın birler basamağı sorulduğundan birler basamağı “0” olan sayı bulunduktan sonra diğerlerine bakmaya gerek yoktur.Cunku diğer sayıların da birler basamağı sıfır olacaktır.0! = 11! = 12! = 23! = 64! = 245! = 1206! = 7201 + 1 + 2 + 6 + 24 = 34 Elde edilen toplamın birler basamağı 4 olduğundan sorulan toplamın da birler basamağı 4 tür.
40. Sayfa
4. KAYNAKLAR1. " Sosyal Bilimler MYO için Temel Matematik" , Prof. Dr. Mustafa SEVÜKTEKİN, Dora Basım Yayın Dağıtım, 20152. " YGS Temel Matematik", Aydın Basın Yayın Matbaa Sanayi ve Ticaret Ltd. Şti., 20123. " ÖSS Matematik ", Mustafa YAĞCI, 20094. " Temel Matematik", Prof.Dr. Mahmut KARTAL, Nobel Yayın Dağıtım, 20095. " Temel Matematik ", Doç.Dr. İrfan ERTUĞRUL, Ekin Basım Yayın Dağıtım, 2012
Tam Sayı Videoları
 5 yıl önce
5 yıl önce
 5 yıl önce
5 yıl önce
